102. 二叉树的层序遍历
102. 二叉树的层序遍历
分析
我最开始的想法,是先用中序遍历遍历所有元素(这样,同一层的左边的元素始终排在这一层右边的元素的前面),同时带高度信息,将遍历结果结果放到一个列表里面,然后从头遍历列表,根据节点的高度,来将节点进行分离。
但是官方答案更巧妙,直接使用队列这个数据结构,具体过程如下:
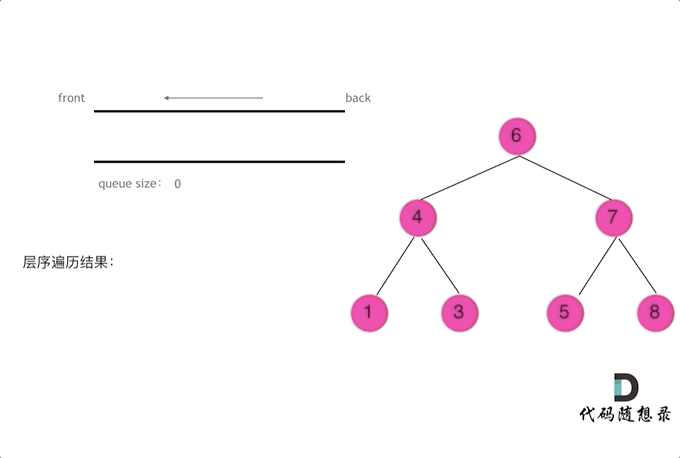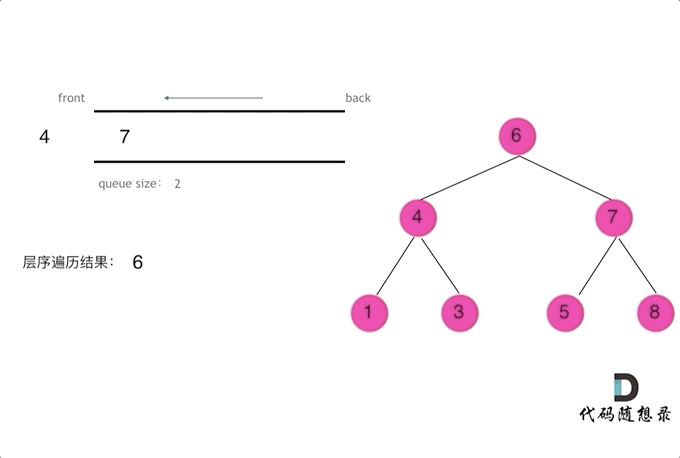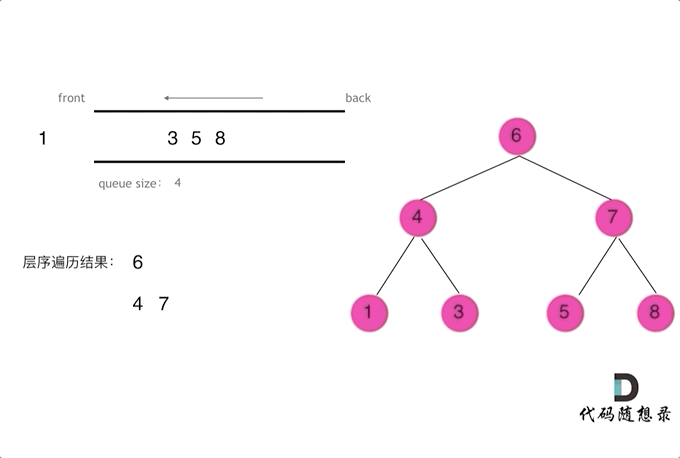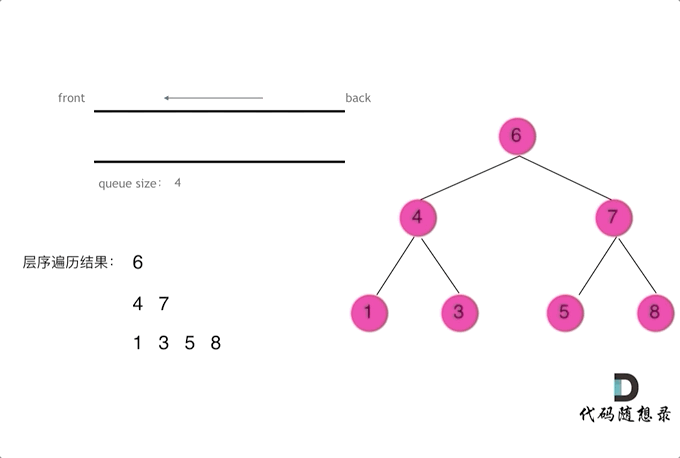
思路是
创建一个队列,并将根节点放入其中,注意根节点可能为空。
- while 循环检查队列是否为空,
- 为空就直接返回,
- 不为空就检查队列的长度,然后用一个 for 循环从队列中读取长度对应个数的元素
- 将将读取到的元素放入一个 List 中,这个 List 就是二叉树中某一层的所有元素。
- 读取的元素的时候将元素对应的节点的子节点重新放入队列中,放心,这不会影响队列的遍历,因为开始 for 循环之前,for 读取的元素的就已经确定了,在 for 的过程中添加的元素不会在本次 for 循环中被读取。
- for 循环结束之后,将这一层的元素放到结果中。
- 回到 while 循环检查队列是否为空
其巧妙的地方在于:
- 每一次 for 循环遍历队列的时候,不是把队列中的所有元素都读取出来(读取队列的时候也在往队列中添加元素),而是只读取开始遍历前的队列的长度的对应的个数的元素,因为这个长度其实就是二叉树某一层元素的个数。所以这就导致虽然我们在不停地往队列中插入元素,但是我们每一次读取的时候,读到的元素都是同一层的,所以这个算法的精髓就在于一次读取的元素的个数。
这个题也可以用递归来做,但是没有那么巧妙,还是用队列来做简洁高明。
层序遍历或者说广度优先遍历的本质,就是一层层的遍历。
解题
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
Deque<TreeNode> queue = new ArrayDeque<>();
if(root!=null){
queue.offer(root);
}
while(!queue.isEmpty()){
// 这里一次循环就是遍历一层的节点
// 获取这一层的长度
int size = queue.size();
List<Integer> list = new ArrayList<>();
for(int i=0;i<size;i++){
TreeNode node = queue.poll();
list.add(node.val);
// 移除一个节点的时候,将其子节点放到队列中
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
result.add(list);
}
return result;
}
}